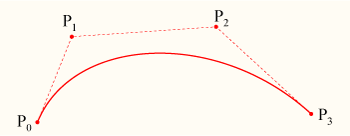
Propiedades y superficies de Bézier

Invarianza afín: La forma de de una curva de Bézier no varía mediante una transformación afín, homotecias, traslaciones y rotaciones.

Envoltura convexa: La curva de Bézier siempre está contenida dentro de la envoltura convexa de los puntos de control.

Simetría: Si invertimos el orden de los puntos de control, la curva de Bézier resultante tras el cambio es la misma pero recorrida en sentido inverso.

Disminución de la variación:El número de intersecciones entre la curva de Bezier y una recta es menor o igual al número de intersecciones de la misma recta con su polígono de control. Intuitivamente, esto nos dice que el polígono de control ya nos da una idea aproximada de por dónde irá la curva.

Pseudo-control local: Si movemos el punto de control Pi a Pi’, entonces todos los puntos de la curva se moverán respecto a la curva original en la dirección del vector PiPi’. Aunque el cambio no afecta a todos los puntos por igual, acentuándose en la zona más cercana al punto P1 en imperceptible en los puntos alejados del mismo.